機(jī)器學(xué)習(xí)模型
有一系列機(jī)器學(xué)習(xí)方法可應(yīng)用于模擬生物反應(yīng)器放大的問題。表 2 列出了這些技術(shù)及其一般優(yōu)缺點(diǎn)。
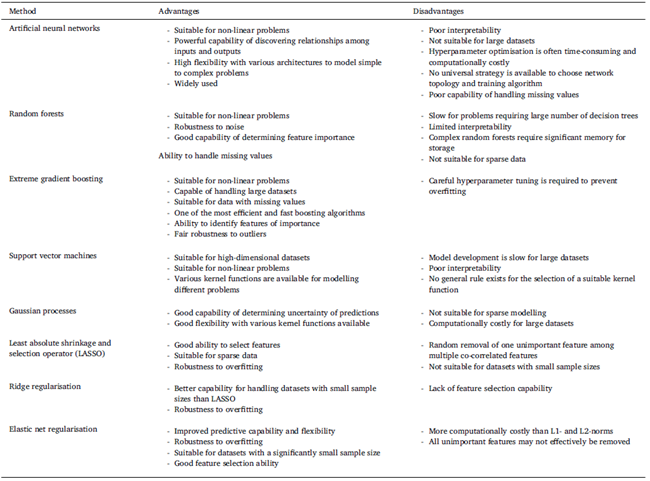
表2. 機(jī)器學(xué)習(xí)方法的一般優(yōu)缺點(diǎn)。
人工神經(jīng)網(wǎng)絡(luò) (ANN) 是最有前途的機(jī)器學(xué)習(xí)技術(shù)之一,可應(yīng)用于生物反應(yīng)器規(guī)模縮放。總的來說,人工神經(jīng)網(wǎng)絡(luò)對(duì)非線性復(fù)雜系統(tǒng)進(jìn)行建模的能力使人工神經(jīng)網(wǎng)絡(luò)成為增長(zhǎng)最快的數(shù)據(jù)驅(qū)動(dòng)生化系統(tǒng)建模方法之一。此外,ANN 模型可以同時(shí)預(yù)測(cè)多個(gè)響應(yīng)變量,同時(shí)也可以將多個(gè)自變量引入輸入層。例如,可以構(gòu)建 ANN 來預(yù)測(cè)生物反應(yīng)器內(nèi)的不同代謝物濃度。
ANN 是由輸入層(第一層)、輸出層(最后一層)和位于輸入層和輸出層之間的隱藏層組成的多層模型。人工神經(jīng)網(wǎng)絡(luò)是高度特定于問題的,并且沒有通用的策略可用于構(gòu)建網(wǎng)絡(luò)拓?fù)洌饕且驗(yàn)椋?/p>
雖然駐留在輸入和輸出層中的節(jié)點(diǎn)數(shù)由自變量和因變量的數(shù)量指定,但沒有一般規(guī)則來確定隱藏層的數(shù)量,且隱藏節(jié)點(diǎn)的數(shù)量根據(jù)問題的復(fù)雜性而變化。
在 ANN 架構(gòu)中,節(jié)點(diǎn)可以完全或部分連接;
傳遞函數(shù)種類繁多,例如線性函數(shù)、S形函數(shù)和雙曲正切函數(shù),用于處理在隱藏層和輸出層中的每個(gè)節(jié)點(diǎn)的輸出值;
有相當(dāng)多的學(xué)習(xí)算法,例如 Levenberg-Marquardt、隨機(jī)梯度下降和自適應(yīng)矩估計(jì),可用于訓(xùn)練模型;以及
還有其它超參數(shù)和層操作,如信息失落、訓(xùn)練迭代次數(shù)、批次大小和學(xué)習(xí)率需要確定
考慮到這一點(diǎn),應(yīng)該采用優(yōu)化策略來調(diào)整網(wǎng)絡(luò)的超參數(shù)并確定其最佳拓?fù)洹_@個(gè)優(yōu)化過程可能很耗時(shí),特別是對(duì)于由高維數(shù)據(jù)集訓(xùn)練的深度神經(jīng)網(wǎng)絡(luò)。
ANN 模型定制的優(yōu)點(diǎn)是這些模型非常靈活,可以用來捕獲各種系統(tǒng)中數(shù)據(jù)的底層結(jié)構(gòu),例如復(fù)雜的生化過程。此外,還開發(fā)了許多其它模型來模擬生物過程,其中包括遞歸神經(jīng)網(wǎng)絡(luò) (RNN)、卷積神經(jīng)網(wǎng)絡(luò) (CNN)、圖神經(jīng)網(wǎng)絡(luò) (GNN) 和徑向基神經(jīng)網(wǎng)絡(luò) (RBNN)。
人工神經(jīng)網(wǎng)絡(luò)已成功用于細(xì)胞培養(yǎng)建模,包括蛋白質(zhì)糖基化的預(yù)測(cè)、培養(yǎng)基成分的優(yōu)化以及預(yù)測(cè)蛋白質(zhì)聚集。此外,一些文獻(xiàn)報(bào)道了使用 ANN 來估計(jì)反應(yīng)器流體動(dòng)力學(xué)。Patel 和 Thibault (2009) 建立了一個(gè)前饋神經(jīng)網(wǎng)絡(luò)來預(yù)測(cè)好氧發(fā)酵中的 kLa 值。作者試圖調(diào)和由不同理論方法確定的 kLa 數(shù)據(jù),即動(dòng)態(tài)方法、穩(wěn)態(tài)方法、氧氣平衡法和二氧化碳?xì)怏w平衡法,而不是對(duì)通過這些方法獲得的 kLa 值進(jìn)行平均。ANN 被證明比其它復(fù)雜的傳統(tǒng)數(shù)據(jù)協(xié)調(diào)算法更簡(jiǎn)單。研究表明,人工神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)的 kLa 值比平均技術(shù)更精確,與傳統(tǒng)數(shù)據(jù)協(xié)調(diào)方法計(jì)算的值相當(dāng)。
在另一項(xiàng)研究中,人工神經(jīng)網(wǎng)絡(luò)被應(yīng)用于預(yù)測(cè)不同的流體動(dòng)力學(xué)和傳質(zhì)參數(shù),例如氣體滯留率、kLa 和氣泡直徑。包含 7,374 個(gè)數(shù)據(jù)點(diǎn)的大型數(shù)據(jù)集由反應(yīng)器幾何形狀、物理化學(xué)特性和操作變量組成,用于訓(xùn)練和測(cè)試開發(fā)的神經(jīng)網(wǎng)絡(luò)。開發(fā)的人工神經(jīng)網(wǎng)絡(luò)在預(yù)測(cè)方面是準(zhǔn)確的,并提供了一個(gè)成功的經(jīng)驗(yàn)相關(guān)性替代方案。
遞歸神經(jīng)網(wǎng)絡(luò)也已用于預(yù)測(cè)哺乳動(dòng)物細(xì)胞生物反應(yīng)器中的關(guān)鍵變量,包括單克隆抗體滴度、活細(xì)胞密度和活性,以及葡萄糖和乳酸濃度。RNN 提供的時(shí)間記憶不是傳統(tǒng) ANN 的特征,這使得 RNN 成為強(qiáng)大的數(shù)據(jù)驅(qū)動(dòng)工具,用于連續(xù)輸入數(shù)據(jù),包括時(shí)間序列數(shù)據(jù),例如代謝物濃度的時(shí)間過程變化。在這項(xiàng)研究中,創(chuàng)建了兩個(gè) RNN 模型,分別命名為特定 RNN 和通用 RNN。特定的 RNN 是根據(jù)從用于生產(chǎn)單一抗體產(chǎn)品的大型生物反應(yīng)器獲得的數(shù)據(jù)進(jìn)行訓(xùn)練的,而通用 RNN 是根據(jù)在小型生物反應(yīng)器中生成的四種不同單克隆抗體產(chǎn)品的組合數(shù)據(jù)進(jìn)行訓(xùn)練的。這項(xiàng)研究的結(jié)果表明,這些模型在計(jì)算不同規(guī)模的細(xì)胞代謝物濃度方面具有適當(dāng)?shù)念A(yù)測(cè)能力。根據(jù)特定過程的數(shù)據(jù)訓(xùn)練的特定 RNN 比通用 RNN 具有更高的準(zhǔn)確性,因?yàn)楹笳呓o出了偏離實(shí)驗(yàn)值的細(xì)胞代謝物和細(xì)胞濃度的預(yù)測(cè)。這對(duì)于預(yù)測(cè)葡萄糖 (R2 = 0.83) 和乳酸濃度 (R2 = 0.95) 最為重要。特定過程中的代謝差異和改進(jìn)的補(bǔ)液策略被認(rèn)為是觀察到的差異的原因。
基于樹的模型也是一類高性能機(jī)器學(xué)習(xí)監(jiān)督算法,可用于描述自變量和因變量之間的高度非線性關(guān)系,使其成為建模本質(zhì)上是非線性的生物系統(tǒng)的潛在工具。基于樹的模型的其它突出優(yōu)勢(shì)包括它們對(duì)缺失值和異常值的不敏感性、它們衡量特征重要性的能力、它們的可解釋性,以及它們?cè)谶^度擬合和欠擬合時(shí)改進(jìn)的穩(wěn)健性。隨機(jī)森林是由多個(gè)并行決策樹組成的基于樹的集成。隨機(jī)森林可用于回歸和分類問題。隨機(jī)森林回歸工具由通過遞歸分區(qū)方法創(chuàng)建的去相關(guān)回歸樹組成。每棵樹都用于根據(jù)獨(dú)立采樣的隨機(jī)向量的值預(yù)測(cè)響應(yīng)。隨機(jī)森林已被用作預(yù)測(cè)蛋白質(zhì)結(jié)構(gòu)的分類器算法,預(yù)測(cè)蛋白質(zhì)-蛋白質(zhì)/配體相互作用,生物反應(yīng)器故障檢測(cè)和微生物網(wǎng)絡(luò)分析。隨機(jī)森林作為預(yù)測(cè)生物量和微生物或細(xì)胞代謝物的回歸工具的應(yīng)用也在多項(xiàng)研究中進(jìn)行了分析, 表明了它們?cè)谀M不同規(guī)模生物反應(yīng)器內(nèi)代謝物濃度的潛力。
梯度提升方法也被認(rèn)為是非常強(qiáng)大的基于樹的集成。這種方法對(duì)異常值具有穩(wěn)健性。該技術(shù)還能夠自動(dòng)合并預(yù)測(cè)變量之間的交互作用。與隨機(jī)森林模型不同,增強(qiáng)算法是一組順序決策樹,這些樹經(jīng)過迭代訓(xùn)練和增強(qiáng),用于重新加權(quán)現(xiàn)有樹集合建模不佳的觀察結(jié)果。
極端梯度提升 (XGBoost) 是一種可擴(kuò)展的樹提升算法,其僅需要最少的計(jì)算資源,具有良好的通用性和高可解釋性。XGBoost 已應(yīng)用于許多系統(tǒng),以識(shí)別生物分子反應(yīng)坐標(biāo),預(yù)測(cè)革蘭氏陰性菌的抗菌素耐藥性,預(yù)測(cè)發(fā)酵產(chǎn)物并確定潛在的抗病毒藥物和抗病毒的中和抗體。
這些基于樹的算法的多功能性已經(jīng)在蛋白質(zhì)工程領(lǐng)域得到證實(shí)并且由于其可解釋性和特征選擇能力,預(yù)計(jì)它們將有相當(dāng)大的潛力為復(fù)雜生物過程開發(fā)策略的未來數(shù)據(jù)驅(qū)動(dòng)評(píng)估做出貢獻(xiàn)。
另一種流行的機(jī)器學(xué)習(xí)方法是支持向量機(jī) (SVM) 分析,它可用于分類和回歸。SVM 模型是一種基于核的非參數(shù)數(shù)據(jù)驅(qū)動(dòng)方法。核函數(shù)用于將原始輸入從原始特征空間轉(zhuǎn)換到更高維空間。SVM 算法中可以使用各種核函數(shù),即線性函數(shù)、多項(xiàng)式函數(shù)、狄利克雷函數(shù)、徑向基函數(shù)和 S 形函數(shù)。與每個(gè)內(nèi)核函數(shù)關(guān)聯(lián)的參數(shù)通過適當(dāng)?shù)男阅軆?yōu)化方法進(jìn)行調(diào)整。SVM 以其處理高維數(shù)據(jù)集的能力而聞名。它們?cè)跒椴煌到y(tǒng)建模時(shí)也具有內(nèi)存效率和靈活性。
除了它們?cè)谏飳W(xué)中廣泛用于預(yù)測(cè)蛋白質(zhì)和酶功能、轉(zhuǎn)錄起始位點(diǎn)的鑒定和基因表達(dá)數(shù)據(jù)的分類之外,一些研究人員已經(jīng)將 SVM 應(yīng)用于生物反應(yīng)器模型。SVM 算法也已用于預(yù)測(cè)不同規(guī)模的生物反應(yīng)器性能。作者開發(fā)了基于內(nèi)核的支持向量回歸和偏最小二乘回歸,以根據(jù)在不同規(guī)模下(包括 80 L、400 L、2,000 L 和12,000 L)的抗體終濃度和乳酸終濃度,分析CHO細(xì)胞培養(yǎng)性能。以 80 L 規(guī)模開發(fā)的模型預(yù)測(cè) 12,000 L 生產(chǎn)規(guī)模生物反應(yīng)器性能的能力低于以 2,000 L 規(guī)模開發(fā)的模型的能力。與每種規(guī)模的單獨(dú)數(shù)據(jù)集相比,跨規(guī)模編譯數(shù)據(jù)并沒有提高預(yù)測(cè)準(zhǔn)確性。這歸因于在較小規(guī)模(即 80 L 至 2,000 L)下獲得的噪聲數(shù)據(jù)。盡管如此,與本研究中同樣檢查的更簡(jiǎn)單的 PLS 模型相比,SVM 模型在處理這些噪聲數(shù)據(jù)方面更加穩(wěn)健,顯示了這種先進(jìn)方法的優(yōu)勢(shì)。
高斯過程算法是另一種非參數(shù)的、基于內(nèi)核的機(jī)器學(xué)習(xí)技術(shù),可應(yīng)用于縮放生物反應(yīng)器。這種方法在確定預(yù)測(cè)的置信區(qū)間方面具有明顯優(yōu)勢(shì)。計(jì)算由平均值和方差表示的正態(tài)分布作為高斯過程模型的輸出。平均值被分配給最可能的預(yù)測(cè)值,而置信區(qū)間由方差確定。然而,對(duì)大型數(shù)據(jù)集使用高斯過程在計(jì)算上可能存在問題。研究人員已成功地將高斯過程應(yīng)用于生物系統(tǒng),以優(yōu)化細(xì)胞培養(yǎng)基、估計(jì)生物量濃度、預(yù)測(cè)時(shí)間依賴性代謝物以及鑒定代謝途徑中的酶。
正則化方法在具有大量相關(guān)參數(shù)的生物系統(tǒng)的數(shù)據(jù)驅(qū)動(dòng)分析中尤其可以發(fā)揮重要作用,因?yàn)檫@些方法同時(shí)考慮了模型擬合和特征選擇。如圖 4 所示,生物反應(yīng)器中可能會(huì)出現(xiàn)不同變量之間的顯著相關(guān)性(稱為多重共線性),這使得這種縮放方法特別有吸引力。盡管多重共線性可能不會(huì)影響模型預(yù)測(cè),但強(qiáng)多重共線性會(huì)導(dǎo)致對(duì)自變量對(duì)響應(yīng)變量影響的嚴(yán)重誤導(dǎo)性解釋,以及不穩(wěn)定和有偏見的統(tǒng)計(jì)分析。基于正則化技術(shù)的懲罰回歸模型的開發(fā)可以減輕這些多重共線性問題。為此,通過以下常用的正則化方法將懲罰項(xiàng)添加到誤差函數(shù)(也稱為損失函數(shù))中:
L1 正則化(也稱為 L1 范數(shù)和最小絕對(duì)收縮和選擇算子 (LASSO))將模型參數(shù)的絕對(duì)值之和合并到懲罰損失函數(shù)中。使用此正則化器,未使用的參數(shù)變?yōu)榱悖灰虼耍ㄟ^消除對(duì)模型的預(yù)測(cè)能力沒有顯著影響的冗余特征來簡(jiǎn)化模型。盡管如此,L1 范數(shù)無法識(shí)別協(xié)變量的正確選擇,而是從多個(gè)相關(guān)變量中隨機(jī)選擇一個(gè)變量。此外,當(dāng)預(yù)測(cè)變量的數(shù)量遠(yuǎn)大于觀測(cè)值的數(shù)量時(shí),L1 范數(shù)無效。
L2 正則化(也稱為 L2 范數(shù)和嶺正則化)將模型參數(shù)的平方值之和納入懲罰損失函數(shù)。與 L1 范數(shù)相比,L2 范數(shù)不排除任何特征,而是降低了最不重要特征的系數(shù)大小。因此,使用 L2 范數(shù)進(jìn)行特征選擇受到限制。
彈性網(wǎng)絡(luò)正則化結(jié)合了 L1 和 L2 正則化方法。由于 L1- 和 L2-范數(shù)的優(yōu)點(diǎn)都包含在彈性網(wǎng)絡(luò)正則化器中,因此它通常優(yōu)于單獨(dú)的 L1- 和 L2-范數(shù)。2003 年提出彈性網(wǎng)的 Zou 和 Hastie 證明了當(dāng)預(yù)測(cè)變量的數(shù)量遠(yuǎn)大于觀測(cè)值的數(shù)量時(shí)彈性網(wǎng)的改進(jìn)能力。
這些正則化方法已應(yīng)用于代謝通量分析和蛋白質(zhì)組學(xué)的特征選擇,以及提供細(xì)胞培養(yǎng)生物反應(yīng)器的簡(jiǎn)化表示。Severson等人 (2015) 利用帶有Monte Carlo采樣的彈性網(wǎng)來預(yù)測(cè)抗體生產(chǎn)過程的滴度和產(chǎn)品質(zhì)量屬性。在 Badsha 等人 (2016) 的研究中,還開發(fā)了 LASSO 和彈性凈回歸模型,以將細(xì)胞生長(zhǎng)、抗體產(chǎn)生、葡萄糖、乳酸、氨離子和谷氨酰胺濃度與 CHO 細(xì)胞的關(guān)鍵細(xì)胞內(nèi)代謝物聯(lián)系起來。比較為每個(gè)模型輸出確定的重疊重要特征,作者指出了基于細(xì)胞代謝的模型輸出之間的可能關(guān)系,顯示了這些數(shù)據(jù)驅(qū)動(dòng)方法在識(shí)別細(xì)胞代謝物之間合理關(guān)聯(lián)方面的潛在用途。






